Ciągi

Ciąg geometryczny (lub postęp geometryczny) – ciąg liczbowy (skończony bądź nieskończony), którego każdy kolejny wyraz od drugiego począwszy jest iloczynem wyrazu poprzedniego przez pewną stałą nazywaną ilorazem. Ciąg geometryczny można traktować jako multiplikatywną wersję (addytywnego) ciągu arytmetycznego.

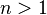Niech $I = \{1, 2, 3, \dots, n\}$ lub $I = \mathbb N$ . Ciąg liczbowy $(a_n)_{n \in I}$ nazywa się ciągiem geometrycznym, jeśli dla dowolnej liczby $n > 1$ zachodzi wzór

a_n = qa_{n-1}

gdzie $q$ jest pewną stałą.

Jeśli $q$ jest różne od zera, to powyższy wzór można zapisać w postaci

\frac{a_n}{a_{n-1}} = q

Własności:

Ponieważ

a_n = qa_{n-1}

to prawdziwy jest też wzór

a_n = q^{n-1} a_1

Każdy wyraz ciągu geometrycznego, prócz pierwszego (oraz ostatniego, jeśli ciąg jest skończony) jest średnią geometryczną wyrazów sąsiednich: jeśli $a_{i-1}, a_i, a_{i+1}$ są trzema kolejnymi wyrazami ciągu geometrycznego $(a_n)$ , z których żaden nie jest pierwszym ani ostatnim, to prawdziwy jest wzór

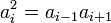a_i^2 = a_{i-1} a_{i+1}