Ciągi

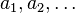Ciąg – przyporządkowanie wszystkim liczbom naturalnym z przedziału $[1, n]$ , lub wszystkim liczbom naturalnym dodatnim, elementów z pewnego ustalonego zbioru. W pierwszym przypadku jest to ciąg skończony, w drugim ciąg nieskończony. Każdej liczbie naturalnej $i$ jest przyporządkowywany tylko jeden element, oznaczany zwykle $a_i$ . Elementy $a_1, a_2, \dots$ zwane są zwykle wyrazami ciągu. W odróżnieniu od elementów zbioru, kolejność wyrazów ciągu jest istotna, a ta sama wartość może wystąpić w ciągu wielokrotnie.

przyklady ciągów:

skończony ciąg pięciu liczb naturalnych: $10,\ 2,\ 3,\ 0,\ 12$
nieskończony ciąg stały: $5,\ 5,\ 5,\ ,\dots$
nieskończony ciąg: $1,\ -1,\ 1,\ -1,\ \dots$
nieskończony ciąg kolejnych liczb pierwszych: $2,\ 3,\ 5,\ 7,\ 11,\ 13,\ 17,\ 19,\ 23,\ \dots$
nieskończony ciąg następujących liczb wymiernych: $\tfrac{1}{1},\tfrac{1}{2}, \tfrac{1}{3}, \tfrac{1}{4}, \dots$
skończony ciąg dużych liter alfabetu łacińskiego: $A,\ B,\ C, \dots,\ Z$